Build the skills your teams need
Give your teams the O’Reilly learning platform and equip them with the resources that drive business outcomes. Click on a feature below to explore.
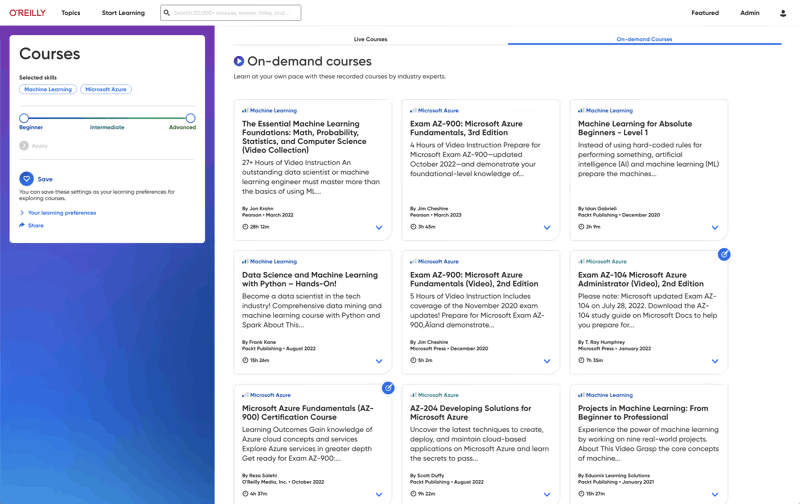
Level up with expert-led live courses
Reserve your seat for interactive workshops to gain hands-on experience—and ask questions along the way.
Pick your eventsO’Reilly AI-powered Answers just got even smarter
O’Reilly Answers instantly generates information teams can trust, sourced from thousands of titles on our learning platform.
Discover AnswersMore than 5,000 organizations count on O’Reilly







O’Reilly Experts
We share the knowledge of innovators. You put it to work.
Tech teams love tapping into the minds of innovators through our expert-led courses, renowned text-based content, and bite-size online Superstream tech conferences. In fact, in a recent survey, one-third of tech practitioners rated O’Reilly content a five out of five (excellent)—better than Pluralsight, LinkedIn Learning, Udacity, or Skillsoft.
Hear why Jose is on O’Reilly every day
Jose, a principal software engineer, trusts our learning platform to filter what his teams need to know to stay ahead.
See why Addison loves our learning platform
Addison always appreciated O’Reilly books, but the learning platform helped take her skills to the next level.
Amir trusts O’Reilly to find the answers he needs. See why.
For over eight years Amir has counted on our learning platform whether he needs proven methods to learn new technologies or the latest management tips.
Mark’s been an O’Reilly member for 13 years. See why.
Mark credits the O’Reilly learning platform with helping him to stay ahead at every turn throughout his tech career.